An Approach to, and Tool for, Predicting the Time Course of an Infectious Disease Outbreak as a Function of Behavioral Interventions

Introduction

Infectious diseases are among the leading causes of morbidity and mortality, worldwide. Starting early twenty-first century, humans have suffered from several serious infectious diseases of animal origin, namely Ebola, Influenza, Severe Acute Respiratory Syndrome Coronavirus (SARS-CoV), and Middle East Respiratory Syndrome Coronavirus (MERS-CoV).¹ For instance, in December 2019, the SARS-CoV-2 was identified first in Wuhan, China causing fever, cough and severe respiratory syndrome in human being.^2,3

Early warning is essential for preventing and controlling outbreaks or epidemics of infectious diseases. However, many decisions rely on subjective expert opinions. To prevent, control, and make early warnings, statistical methods are indispensable for establishing appropriate models, ranging from early warnings to controlling infectious diseases. Such statistical models are also acknowledged by the WHO as they play a key role in evidence-based decisions.⁴ In this regard, different epidemic models have been proposed to study the spread of infectious disease outbreaks.^5–7 Epidemic models are powerful tools used to assess the dynamics of infectious diseases and design possible control measures in a timely manner. Recently, different non-pharmaceutical intervention approaches have been implemented to reduce the spread of coronavirus (Covid-19).^8–12 The model projections of such approaches are subjective and often change because epidemic models rely on assumptions about human behavior, such as the frequency of social contact.

In the absence of pharmaceutical interventions, such as a safe and effective human vaccine, efforts have focused on implementing non-pharmaceutical interventions. These include social distancing, face mask usage, hand washing, quarantine of suspected cases, and hospitalization of confirmed cases. Strict social-distancing measures have been the primary tool for curbing the spread of the pandemic. Face masks have long been utilized to limit the spread of respiratory diseases within the population. Several countries have employed combinations of non-pharmaceutical interventions to reduce the spread of SARS-CoV-2 transmission.^13,14

Epidemic models are usually difficult to implement by researchers and decision-makers without a strong background in statistical modeling. Therefore, because of the increasing need to estimate the incidence and assess the effects of interventions with various appropriate warning models in a single environment, this paper provides a simple user-friendly tool for predicting the incidence of infectious disease outbreaks using various improved epidemic models. The interactive computer program includes the main non-pharmaceutical interventions implemented to limit infectious transmission in a community (ie, social distancing, hand washing, and use of face masks). This tool helps users to produce plots of new projected cases and cumulative cases of infections over a period of time, as well as of the projected cumulative number of deaths and recoveries occurring over a period of time, as a function of several possible interventions. A manual is presented in the Appendix with descriptions running in a MATLAB environment. Although the manual can be considered part of the manuscript, it can be consulted independently.

The improved epidemic models are described as follows. Thereafter, an example was used to demonstrate the software application and the different decisions that users must make when estimating the incidence. Finally, a discussion and conclusions are presented.

Epidemic Models

The most common infectious disease forecast and warning models are susceptible–infectious–removed (SIR), susceptible–infectious–susceptible (SIS), and susceptible–infectious–recovery–susceptible (SIRS). Currently, the COVID-19 outbreak has been widely modeled using the classical SIR model to analyze the epidemic situation. The SIR model, initially introduced by Kermack and McKendrick,¹⁵ is a compartmental model used to predict disease outcomes when individuals obtain permanent immunity after an infection. This model divides the population into three subpopulations: individuals who are not infected (susceptible S), infected individuals with symptoms that can transmit the disease (I), and removed individuals (R) containing recovered and dead people. However, the SIR model is inappropriate for diseases with a latent stage (exposed individuals) such as COVID-19. This model can be extended to each of the following five extras, resulting in 32 possible models (Figure 1):

Figure 1 The various improved SIR models. Interv.: Intervention. Only models in the rounded bigger rectangles are discussed in this paper.

Extra 1: Death (SIDR).

Extra 2: Re-infection (SIRS).

Extra 3: Exposed but not yet infectious (SEIR).

Extra 4: Quarantine (SIQR).

Extra 5: Interventions (SIR with Interventions).

Improved SIR Models

In the next section, we introduce improved SIR models that incorporate the main non-pharmaceutical interventions implemented to limit COVID-19 transmission (ie, social distancing, hand washing, and use of face masks). Figure 1 shows the various improved SIR models. First, we describe the general epidemic model that contains all the extras in it. Thereafter, we present sub-models that include the extra death (D) and one of the other extra’s, which can be obtained from the general model by setting certain parameters to zero.

SEIQDRS Model

In this section, we introduce an improved SIR model that contains all the extras in it (see Figure 1), including the main non-pharmaceutical interventions that have been implemented to limit COVID-19 transmission in a community setting (ie, social distancing, hand washing, and use of face masks). The SEIQDRS model is an extensive model used to predict infectious disease dynamics by subdividing the total population size (N) at period t into six mutually exclusive compartments: susceptible (S(t)), exposed (E(t)), infectious (I(t)), quarantined (Q(t)), death (D(t)), and recovered (R(t)). Furthermore, this model allows individuals to acquire immunity only for a certain period after infection (ie, recovered individuals gain no permanent immunity and can be re-infected by the disease in the future). It also considers that infected individuals are not instantly infectious; hence, the exposed segment apart from the infectious one. Moreover, this model distinguishes quarantined/isolated infected individuals from non-isolated ones. In this model, we assumed that isolated infected individuals are removed from the population and cannot infect new individuals while they remain isolated. The SEIQDRS model with the main non-pharmaceutical interventions implemented to limit COVID-19 transmission in a community setting (ie, social distancing, hand washing, and use of face masks) is shown in Figure 2.

Figure 2 Model flow for the SEIQDRS model with interventions.

The improved model consists of the following system of differential equations:

(1)

(2)

(3)

(4)

(5)

(6)

where θ is the incubation rate, which describes the rate at which the exposed individuals develop symptoms (the transition rate from exposed to infectious class); δ is the rate of quarantine; κ is the rate at which infected individuals die if not quarantined; and π is the rate at which the infected non-quarantined individuals recover. Parameter β is the rate of recovery among quarantined individuals. Parameter γ is the death rate among infected quarantined individuals and ρ is the fixed rate at which recovered individuals return to the susceptible group. Finally, susceptible (S) individuals become exposed to the virus at time t at rate Λ, a parameter known as the force of infection rate, is defined as.

(7)

where α is the effective transmission rate from susceptible to exposed (probability of infection per contact), Λ depends on the prevalence of infection (I(t)/N) and the probability of transmission parameter (α), N is the total population size (=S(t)+E(t)+I(t)+Q(t)+D(t)+R(t)), t is time measurement (eg, day, week, month), 0 < φ ≤ 1 is the effectiveness of social distance, 0 ≤ µ ≤ 1 is the coverage of social distance (ie, the amount of use of social distancing by the community), 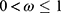is the effectiveness of face masks, is the coverage of face mask usage, 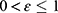is the effectiveness of hand washing, and is the coverage of hand washing. Social distancing minimizes the rate of contact between individuals, hand washing prevents the spread of infectious diseases, while face-mask use reduces the chance of infection given contact, all leading to a lower force of infection. If , or (so if at least one intervention is very effective and has good coverage), the force of infection drops strongly; that is, Λ goes to 0. Conversely, if all three terms go to zero (none of the interventions are effective and implemented with good coverage), Λ goes to , and this model reduces to the SEIQDRS model without interventions.

SIQDR Model

Here, we introduce an improved SIR model that includes Extra 1 and 4 (Figure 1). This model, shown in Figure 3, assumes that there is no latent period for the onset of infectiousness. Infected individuals are instantly infectious and can obtain permanent immunity after the infection. The SIQDR model reflects the effect of quarantine/isolation of infected individuals on the time course of infections, in comparison with the SIDR model. The SIQDR model comprises five compartments: susceptible (S), infected (I), quarantined (Q), death (D), and recovered (R). This model can be obtained by setting θ=1 and ρ=0 in the SEIQDRS model (Table 1).

Table 1 The Different Sub-Models, Which Can Be Obtained From the General SEIQDRS Model by Setting Certain Parameters to Zero

Figure 3 Model flow diagram for the SIQDR model.

By setting Λ = 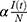, this model reduces to the SIQDR model without interventions.

SEIDR Model

This is an improved SIR model that includes extras 1 and 3 (Figure 1), and does not distinguish quarantined/isolated infected individuals from non-isolated ones. This model, shown in Figure 4, can be used for diseases when recovered individuals acquire permanent immunity and there is a latent period prior to the start of infectiousness. The SEIDR model can be obtained from the SEIQDRS model by setting ρ=0 and δ=0 (see Table 1).

Figure 4 The SEIDR model flow chart.

SIDRS Model

This model contains the extras 1 and 2 and assumes (a) the absence of quarantine (δ=0) or of any effect of quarantine (κ = γ) and π = β), (b) all exposed persons are infectious (θ=1), and (c) individuals do not acquire permanent immunity after recovery (ρ > 0). The SIDRS model consists of four compartments (Figure 5): susceptible (S), infectious (I), death (D), and recovered (R).

Figure 5 The SIDRS model flow chart.

SIDR Model

The SIDR model can be obtained by setting ρ=0, θ=1, and δ=0 in the SEIQDRS model and can be used when individuals (a) obtain permanent immunity after infection, (b) there is no latency between exposure and infectiousness, and (c) there is no quarantine or no effect of quarantine. The scheme is illustrated in Figure 6.

Figure 6 The SIDR model flow chart.

The choice ρ=0, θ=1, δ=0, and κ= 0 in equations 1–6 gives the classic SIR model.

Example

As an illustration of the application and to discuss the different decisions that the user has to make when predicting the prevalence of an infectious disease as a function of time since the outbreak, we consider the SEIDR model and input parameter values from recent studies in Table 2. This model is used when individuals can obtain permanent immunity after infection and assumes that (a) there is a latent period prior to the start of infectiousness and the model assumes that there is no quarantining (δ=0) or no effect of quarantining (κ = γ and π= β).

Table 2 Parameters and Assumptions Used to Run the Modeling Scenarios for SEIDR Model with Interventions (the Non-Pharmaceutical Interventions)

Modeling Scenarios

We considered the following eight scenarios to assess their potential impact on the COVID-19 pandemic:

Scenario-1: No social distancing, No face mask usage, No hand washing.

Scenario-2: No social distancing, No face mask usage, 80% hand washing.

Scenario-3: No social distancing, 80% face mask usage, No hand washing.

Scenario-4: No social distancing, 80% face mask usage, 80% hand washing.

Scenario-5: Social distancing, No face mask usage, No hand washing.

Scenario-6: Social distancing, No face mask usage, 80% hand washing.

Scenario-7: Social distancing, 80% face mask usage, No hand washing.

Scenario-8: Social distancing, 80% face mask usage, 80% hand washing.

The SEIDR model is used for the eight scenarios described above. Based on a population of 300,000 residents, model projections are given for the daily number of infections (Figure 7) and cumulative number of infections (Figure 8) over time. For Scenario-1, where no interventions (No Social distance, No Face mask and No hand washing) are taken at all, the epidemic is projected to reach a peak after 61 days, with an estimated number of new infections of 85,288 individuals (28.4% of the population can be infected) (Figure 7), and the total cumulative number of infections reached in a 100 days is 298,887 (99.6% of the population can be infected) (Figure 8). The total number of deaths is 8,908 at 100 days (Figure 7).

Figure 7 Continued.

Figure 7 Projected number of COVID-19 infections for the eight scenarios. Panels show infections with no social distancing measures assumed (left column) and with social distancing assumed (right column). Abbreviations: SD, Social distance; FM, Face mask; HW, Hand washing. Note: Plot 8 has a different Y-scale because with the same scale as in the other plots, plot 8 would become empty as all lines are entirely below Y=300.

Figure 8 Continued.

Figure 8 Projected cumulative number of COVID-19 infections. Panels show cumulative infections with no social distancing measures assumed (left column) and with social distancing assumed (right column). Note: Plot 8 has a different Y-scale because with the same scale as in the other plots, plot 8 would become empty as the line is entirely below Y=1800.

On the other hand, an intervention that combines social distancing, 80% coverage in the use of face masks, and 80% coverage of hand washing (Scenario-8) leads to an estimated number of new infections of 18 individuals over 100 days. The total number of deaths is two in 100 days, which is a dramatic decrease of 99.98% compared with the scenario of no interventions (Figure 7). The total cumulative number of infections under Scenario 8 is 105 (0.035% of the population infected) over 100 days (Figure 8).

Discussion

Early warning is a crucial measure during infectious disease outbreaks, essential for controlling and preventing outbreaks and epidemics. Accurate and reliable predictions of infectious disease dynamics are invaluable to public health organizations when planning interventions to decrease or prevent disease transmission. Epidemic models are powerful tools for assessing the dynamics of infectious diseases and effects of possible control methods in a timely manner. However, implementing these models is often challenging without a strong background in statistical modeling. Consequently, most decisions are based on expert opinions rather than robust epidemiological model outputs.

To address this, we present a user-friendly tool designed to predict the time course of an infectious disease outbreak based on behavioral interventions, using various improved epidemic models applicable to disease prevention and control. Recent literature was reviewed to identify the key parameters relevant to illustrating the program. In a hypothetical example, combining social distancing with 80% coverage of face masks and hand washing reduced transmission by 99.96% and the death rate by 99.98% compared to the scenario of no preventive measures. Our results demonstrate that non-pharmaceutical interventions (social distancing, hand washing, and face mask usage) not only lower the force of infection and death rates, but also reduce the accumulation of cases and delay the peak transmission time. This enables hospitals and healthcare systems to better manage severe and critical cases. Our findings support recent data that indicates non-pharmaceutical interventions are beneficial against SARS-CoV-2 epidemics.^12,17–19

This interactive computer program will help epidemiologists, public health experts, and decision-makers in better understanding and predicting the time course of infectious disease outbreaks and the effects of preventive measures on infectious disease outbreaks. It is also helpful for generating rapid reports and predictions in outbreak situations where a fast response is required. Moreover, it will improve collaboration between public health and modeling professionals, with the objective of optimizing disease prevention and control strategies. The computer program EpiModeling_Infectious runs in MATLAB and can be obtained upon request from the corresponding author, with potential future availability via the internet. Our current models do not differentiate between symptomatic and asymptomatic infections. Future extensions of the epidemic models and software could include separate considerations for symptomatic and asymptomatic infections.