Introducing Angle B: A Novel Quantitative Approach for Sagittal Alignment Reduction in Atlanto-Axial Dislocation Surgery

Introduction

Atlantoaxial dislocation (AAD) is a pathological condition characterized by the abnormal anatomical alignment of the atlas (C1) with the axis (C2), leading to instability and joint dysfunction. AAD can lead to nerve compression, and a range of clinical manifestations, from minor axial neck pain to severe complications that can even result in death.^1–4 The classification of AAD has been a subject of debate among spine surgeons, with various systems proposed to categorize the disorder based on different imaging modalities and clinical presentations.

Historically, Greenberg¹ was the first to categorize AAD into two types: reducible dislocation and irreducible dislocation. This initial classification was based on the ability to reduce the dislocation through manual traction or skull traction. In 2021, Shan et al⁵ proposed a more nuanced classification system that incorporated radiographs, reconstructive computed tomography (CT), and the outcome of skeletal traction. Their system aimed to provide a more detailed understanding of the dislocation’s severity and its response to non-surgical interventions. More recently, there has been a move towards classifications that consider the three-dimensional aspects of AAD, including anterior-posterior, vertical, and rotational components. These classifications take into account the complex interactions between the atlas and axis and their impact on the surrounding neural structures.^6–10

The surgical management of AAD is multifaceted, involving correction of anterior-posterior dislocation (sensu stricto AAD), vertical dislocation (basilar invagination), and sagittal alignment of the upper cervical spine. Over time, surgeons have developed various surgical approaches for AAD, which have been described in several studies.^6–10 Despite ongoing debate over the optimal surgical approach, the primary objective remains consistent: to correct anterior-posterior and vertical dislocation, restore sagittal alignment of the upper cervical spine, reconstruct the stability of the atlantoaxial structure, alleviate spinal cord compression, and improve neurological symptoms.

With the advancement in spine biomechanics, there has been growing emphasis on correcting the sagittal alignment of the cervical spine. Numerous studies have explored the influence of cervical sagittal alignment on various spinal diseases, such as cervical spondylotic myelopathy, scoliosis, and ankylosing spondylitis.¹¹ Despite some studies investigating cervical sagittal alignment in AAD, there is still a lack of established knowledge on the correlation between horizontal gaze and quantitative reduction surgery.

In our previous study, we showed that the change of clivo-axial angle (CXA) was equivalent to the change of cervical lordosis (CL) based on two assumptions. Firstly, sagittal spine alignment aims to maintain horizontal gaze. Secondly, deformities at the craniovertebral junction have a minimal effect on the slope of the T1 vertebra.¹² However, CXA, the angle between extension lines of the posterior edge of axis and clivus, does not directly reflect the relationship between the position of the axis and horizontal gaze. Therefore, this study aims to establish a quantitative relationship between cervical lordosis (CL) and the rotation angle of the axis (ΔB) to optimize the surgical reduction process for atlantoaxial dislocation (AAD). We hypothesize that by introducing the angle B and deducing the equation ΔB = ΔCL = D, surgeons can achieve more precise and effective surgical reductions in patients with varying extents of AAD. This equation is expected to provide a crucial tool for preoperative planning and selecting appropriate surgical techniques based on individual patient metrics.

Methods

Participants

Prior to conducting the study, we performed a statistical power analysis to determine if the sample size was sufficient to detect a clinically meaningful effect size. We set the effect size to 0.5, the significance level to 0.05, and the power level to 0.8. Based on these parameters, we calculated the required sample size to be 23 cases, which matches the number of subjects we actually included in the study. We conducted a retrospective study of patients who had undergone posterior reduction and fixation for AAD at our Hospital from 2012 to 2016. To ensure a comprehensive analysis, we categorized the severity of AAD in our patient cohort based on established classification systems that consider the degree of dislocation and neurological involvement. This classification was crucial for determining the appropriate surgical intervention for each patient. As this was a retrospective study, no random allocation was performed. All study subjects underwent the same specific surgical procedure within the defined period, ensuring uniformity and comparability of the groups. All patients underwent detailed preoperative evaluation before being included in the study to ensure the comparability of baseline characteristics. The inclusion criteria for this study were: 1) patients who had undergone posterior reduction and fixation for AAD, and 2) patients with complete pre- and post-operative computed tomography (CT) scans. Exclusion criteria were as follows: 1) patients who had undergone other surgical techniques, 2) patients who had undergone revision surgery, and 3) patients with other craniocervical junction malformations. This study involved human subjects and received approval from the Ethics Committee of our Hospital. All participants provided informed consent before their inclusion in the study.

Surgical Treatment

The surgical approach for each patient was tailored based on the severity of their AAD. For patients with mild to moderate AAD, a posterior reduction and fixation procedure was performed. This involved the use of lateral mass screws and rods for stabilization. In cases of severe AAD with significant vertical dislocation, additional steps such as facet joint release and cage implantation were incorporated to facilitate reduction and decompression of the neural elements.

It is important to note that the severity of dislocation did influence the treatment methods among the selected patients. Patients with more severe dislocations required more complex surgical interventions to achieve reduction and stabilization. Our surgical team made these determinations based on preoperative imaging studies, particularly CT scans, which provided detailed information on the extent of dislocation and any associated bony abnormalities.

Variables and Measurement

We measured the following variables using pre- and post-operative CT images: Slope of T1 Vertebra (T1S): The T1 slope was measured as the angle between the horizontal line and the superior endplate of the T1 vertebra; Slope of Frankfort Horizontal Line (sFH): The slope of the Frankfort horizontal line was measured as the angle between the Frankfort horizontal line (a line passing through the orbitale and the porion) and the horizontal plane; Lower Cervical Lordosis (CL): The lower cervical lordosis was measured as the Cobb angle between the inferior endplates of the C2 and C7 vertebrae.

Angle B: Angle B was measured as the angle between the Frankfort horizontal line and the extension line of the posterior edge of the axis (C2 vertebra). Additionally, we made the following adjustments and calculations: Corrected Cervical Lordosis (cCL): CL was corrected into cCL as previously reported,¹² Change in Cervical Lordosis (ΔCL): The change in cervical lordosis was calculated as the difference between the pre-operative and post-operative CL;Change in Angle B (ΔB): The change in Angle B was calculated as the difference between the pre-operative and post-operative Angle B. To ensure the accuracy and reliability of the measurements, two independent researchers measured all images twice without knowledge of each other’s findings. The consistency of the measurements was assessed using Intraclass Correlation Coefficient (ICC) to ensure intra- and inter-observer reliability.

Software and Statistical Methods

We used Surgimap (Version 2.3.2.1) to view and measure CT images. Pattern diagrams were painted using Easy Paint Tool SAI (Version 2.0). Linear regression was performed using GraphPad Prism (Version 9.0.0) to calculate R² (R-squared) and p-values. A linear fitting equation with an R² value greater than 0.8 and a p-value less than 0.05 was considered a good linear fit.

Results

The Cervical Sagittal Angles Correlation

As shown in Figure 1, we obtained the equation T1S=FXA+CL+sFH. Further deductions led us to the equation T1S+C-sFH=CL+B. Previous studies have reported that, for a normal human, the mean of sFH is 0.5. In addition, T1S is a relatively constant value in cervical spine surgery, while the angle C, which refers to the angle between the inferior endplate and extension line of the posterior edge of the axis, is invariant for everyone. As a result, we can deduce that ΔCL=- ΔB.

Figure 1 Measurements of cervical sagittal angles. The slope of the Frankfort horizontal line (sFH), the angle between the Frankfort horizontal line and the extension line of the posterior edge of the axis (B), the Cobb angle between the inferior endplate of C2 and C7 vertebrae (CL), the slope of the T1 vertebra (T1S), the angle between the Frankfort horizontal line and the inferior endplate of the axial vertebra (FXA), and the angle between the inferior endplate and extension line of the posterior edge of the axis (C) are shown. The dashed lines indicate a horizontal orientation.

Validation of the Correlation Between ΔCL and ΔB

We enrolled a total of 23 patients in this study according to our inclusion criteria, and Table 1 presents the preoperative and postoperative measurements of T1S, sFH, CL, cCL, and B. Additionally, we computed the values of ΔCL and ΔB for each patient. We then utilized a regression analysis to examine the correlation between ΔCL and ΔB (Figure 2). Our study results demonstrated a strong linear relationship between the change in cervical lordosis (ΔCL) and the change in angle B (ΔB) (equation: y=−1.0402x, coefficient of determination R²=0.978, P<0.001). This finding directly supports our goal of establishing a quantitative method to guide preoperative planning for atlantoaxial dislocation surgery. Therefore, we conclude that the equation ΔCL=- ΔB holds.

Table 1 Measurement of Pre- and Postoperative Parameters

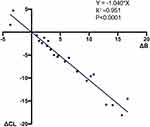Figure 2 Linear regression of ΔCL and ΔB is presented.

The Utility of the Equation in Pre-Surgical Decision-Making

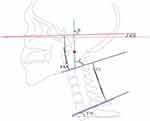
Figure 3A–C illustrate the cervical parameter pattern diagrams of a patient with atlantoaxial dislocation before and after surgery. In particular, D represents the rotation angle of the axis, and Bʹ represents the angle between the FH line and the extension line of the posterior edge of the axis after the operation. Through a series of derivations and transformations, we derived the equation Bʹ=D+B: (1) 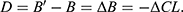Figure 3B, 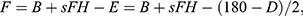and 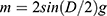. g represents the length of the posterior edge of the axis.

Figure 3 The pattern diagram of the sagittal parameter of the cervical spine and demonstration of the utility of equations in pre-surgical decision-making. (A) Shows the complete view of the sagittal parameter of the cervical spine, with the arcus anterior of atlas represented by a yellow rectangle and the vertex of dens represented by a circle. The dot-dashed lines depicts the postoperative extension line of the posterior edge of the axis and the inferior margin of the axis. Additionally, the red circle with a dotted blue outline displays the ideal location of the vertex of dens after the operation. The dashed lines represent a horizontal orientation. B’ denotes the angle between the Frankfort horizontal line and the extension line of the posterior edge of the axis after the operation, while D indicates the rotation angle of the axis. In (B), a local enlarged image of the dashed black square in Figure 3A is presented with the slope of the Frankfort horizontal line (sFH) translated vertically downward. The length of the posterior edge of the axis (g), length of the line connecting the location of axis before and after the rotation (m), the angle between the posterior edge of the axis and m (E), and the angle between m and horizontal line (F) are labeled. (C) shows a further enlarged image of the dashed black square region in Figure 3B. (D and E) Display pre- and postoperative CT images demonstrating the reduction of AAD of Patient 8.

Moreover, Figure 3C resolves the atlantoaxial interval (m) into the vertical dimension (h) and horizontal dimension (d). Using triangular functions, we can calculate the length of h and d as h=sinFm and d=cosFm. Finally, the equation for h is expressed as: (2) 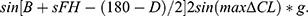d is expressed as (3)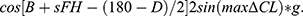

In conclusion, the maximum displacement of the axis can be determined by the maximum ΔCL, which is essential in deciding whether the patient can achieve a theoretical reduction. It is noteworthy that the normal value of CL remains uncertain. However, maintaining a T1S-CL range between 14.5° and 26.5° has been reported as necessary for horizontal gaze.¹³ Therefore, we can calculate the maximum ΔCL based on the normal range of T1S-CL.

Figure 3D displays a preoperative CT image of a 43-year-old female with AAD (ADI=4.50 mm, vertical dimension=1.78mm, horizontal dimension=4.14mm). Her T1S-CL and length of the posterior edge of the axis were 4.3° and 28mm, respectively. According to the range of T1S-CL (14.5° to 26.5°), her maximum ΔCL should be 22.2°. Using the equations, we calculated the theoretical h and d to be 0.8mm and 10.75mm, respectively, which was adequate to reduce her ADI to a normal value (<3mm). Figure 3E shows the postoperative CT image of the patient, indicating a successful reduction of her AAD. Furthermore, her T1S-CL became 21.7°, which falls within the normal range required to maintain horizontal gaze.

Discussion

Our study introduced a novel quantitative method for reducing sagittal alignment in patients with AAD. The key equation (ΔB=ΔCL=D) enables precise preoperative planning and improves surgical outcomes by guiding accurate reductions based on maximum cervical lordosis. Our study findings align well with our objectives and are directly relevant. The linear relationship observed between cervical lordosis and angle B, along with the derived equation, directly supports the goal of this study to establish a quantitative method to guide preoperative planning for this surgery. This correlation is supported by the statistical data, reinforcing the plausibility of the proposed approach. However, we recognize the need for further studies to validate these preliminary findings and explore their applicability in different patient populations and clinical settings.

Cervical Sagittal Alignment

With the advancement of our understanding of spine biomechanics, greater attention has been directed towards cervical sagittal alignment and its impact on clinical outcomes in patients.¹⁴ Sakai et al¹⁵ reported that cervical sagittal imbalance represents a preoperative risk factor for kyphotic deformity following laminoplasty for cervical spondylotic myelopathy. Lee et al¹⁶ further established that cervical sagittal parameters differed significantly between patients with ankylosing spondylitis and healthy controls, with the C2-C7 sagittal vertical axis emerging as a significant predictor of quality of life in patients with this condition. To improve cervical spine deformity classification, Ames et al¹⁷ utilized a modified Delphi approach with an expert panel to develop an updated system that incorporated various cervical sagittal alignments.

In relation to AAD, Zhang et al¹⁸ reported that AAD patients with a postoperative C0-C2 angle of 10–20° exhibited better clinical outcomes. Additionally, Wang et al¹⁹ observed statistically significant negative correlations between the occiput-C2 and C2-C7 angles. Chandra et al²⁰ found a significant correlation between sagittal joint inclination and craniocervical tilt and severity of basilar Invagination and AAD.

Sagittal spinal alignment is a crucial factor that impacts human health and quality of life, as maintaining a horizontal gaze is a vital function for healthy individuals.²¹ Surrogate measures have been developed to evaluate horizontal gaze, with sFH representing a well-established option.²² Hasegawa et al²³ measured the sagittal spinal alignment of 136 healthy subjects and demonstrated that sFH remains stable among the healthy human population (mean = 0.5°).

Quantitative Reset Principle

The reduction of AAD mainly encompasses three aspects: anterior-posterior dislocation (sensu stricto AAD), vertical dislocation (basilar invagination), and sagittal alignment of the upper cervical spine (CXA or angle B). Building upon this foundation, we have proposed a new quantitative reset principle to aid surgeons in selecting an optimal surgical approach. (1) Horizontal dislocation: Rotating the dens with the lateral mass as the pivot by cantilever technique⁶ or C0/1-C2 compression,¹⁰ leading to the anterior movement of the dens. Anterior-posterior reduction distance depends on the dens rotatable angle. According to the previous equations, the dens rotatable angle negatively correlates with CL; thus, the anterior-posterior reduction distance depends on CL. (2) Vertical dislocation: a. When horizontal and vertical dislocations exist, rotating the dens with the lateral mass as the pivot can also reduce part of the vertical dislocation. The remaining vertical dislocation can be reduced by subsequent distraction between the C0/1 and C2 pedicle screws⁶ or inter-articular distraction;^24–26 b. If the horizontal dislocation distance is relatively small (the extreme case is the Geol B type basilar invagination, which does not have a horizontal dislocation), reduction of vertical dislocation can only be achieved by distraction technique; (3) Reduction of CXA/angle B: according to the above geometric relationship, the maximum theoretical reversible amount of CXA/angle B is determined by the CL. Meanwhile, since reduction of CXA/angle B requires forward rotation of the dens which needs a certain horizontal dislocation distance, reduction of CXA/angle B depends on horizontal dislocation distance. The extreme case is the Geol B type basilar invagination, which could not obtain an ideal reduction of CXA/angle B since it has no horizontal dislocation.

The Use of Equations in Clinical Practice

This study introduces the concept of angle B and deduces the equation ΔB=-ΔCL, which has been retrospectively verified by analyzing cases from our center. Our previous study indicated that ΔCXA equaled ΔCL. While our previous study showed that ΔCXA equates to ΔCL, CXA only reflects the angle between the extension lines of the posterior edge of axis and clivus, and not the axis location in relation to the horizontal gaze.

On the other hand, B represents the angle between the Frankfort horizontal line and the extension line of the posterior edge of axis, and directly reflects the axis location with respect to the horizontal gaze. Additionally, the equation ΔB=D is derived, indicating that a patient’s maximum ΔCL determines the maximum angle of rotation of the axis. These equations enable us to calculate the maximum vertical and horizontal distance that the axis can move using trigonometric functions. In summary, a patient’s CL “potential” determines whether they can achieve an ideal reduction.

In conclusion, for patients whose theoretical length “m” exceeds the atlantoaxial interval, the typical direct posterior reduction can be performed. Meanwhile, if the length “h” is shorter than the vertical distance between the axis and the arcus anterior of atlas, facet joint release and cage implantation techniques may be used to vertically move the axisx over a longer distance.²⁷

Limitations

There are several limitations to our study that should be acknowledged. Firstly, our study is retrospective in nature, and thus, it is imperative to conduct prospective research to confirm our findings. Secondly, the images were obtained using CT scans rather than upright standing images, which would be more ideal for assessing the relationship between cervical alignment and horizontal gaze. Future studies should aim to obtain axial skeleton imaging of patients with AAD in an upright and horizontal position to provide a more accurate assessment. Thirdly, to enhance the generalizability and external validity of our study results, future studies should consider including a larger patient population. While our study provided promising results in a sample of 23 patients, we acknowledge that this relatively small sample size may limit the generalizability of our findings. Therefore, we recommend that future studies should be conducted in larger and more diverse patient populations to validate our results and further explore the application of angle B in different patient groups. Additionally, future studies should also consider including long-term follow-up data to assess the durability of surgical outcomes.

Conclusion

In conclusion, our study introduces a novel quantitative approach to the reduction of sagittal alignment in patients with AAD. The establishment of the equation (ΔB=ΔCL=D) allows for precise determination of the theoretical reduction achievable based on maximum CL. This equation serves as an essential tool for preoperative planning and selecting appropriate surgical techniques for patients with varying extents of AAD. It guides surgeons to achieve accurate and effective surgical reductions, thereby improving AAD surgery outcomes. To integrate these findings into clinical protocols, we recommend including the measurement of angle B in preoperative assessments and using the ΔB=ΔCL=D equation to guide surgical planning. This approach can help surgeons more accurately predict and plan the surgical reduction process, potentially improving patient surgical outcomes.